Christoph Reuter: Statistische Auswertung mit JASP und GPower

Statistische Auswertung von erhobenen Daten mit JASP

JASP ist die Abkürzung für "Jeffrey’s Amazing Statistics Program", das einen enorm intuitiven Zugang zur statistischen Auswertung von erhobenen Daten bietet und die meisten statistischen Verfahren beinhaltet, die man in der Systematischen Musikwissenschaft benötigt.

Das seit 2013 an der Universität Amsterdam entwickelte Programm für
- Windows (https://jasp-stats.org/thank-you-for-downloading-jasp-win64),
- Mac (https://jasp-stats.org/thank-you-for-downloading-jasp-macos) und
- Linux (https://jasp-stats.org/linux-installation-guide/)
ist frei unter https://jasp-stats.org erhältlich.

Nach der Installation kann es über Menü -> Öffnen -> Computer Daten (z.B. aus Excel exportiert) als .csv (character separated values), .tsv (tab separated values), .txt (einfache Textdateien), .ods (open document spreadsheat) und .sav (SPSS-Dateien) laden.

Daten einladen in JASP

Nach dem Laden liegen die Daten wie in einer Excel-Tabelle vor. In den Spalten wird angezeigt, ob es nominale (= statistisch nicht auswertbare) Daten sind, ordinale (=sortierbare aber nicht zählbare) Daten sind, oder metrische (= zählbare, in gleichen Abständen vorliegende) Daten.

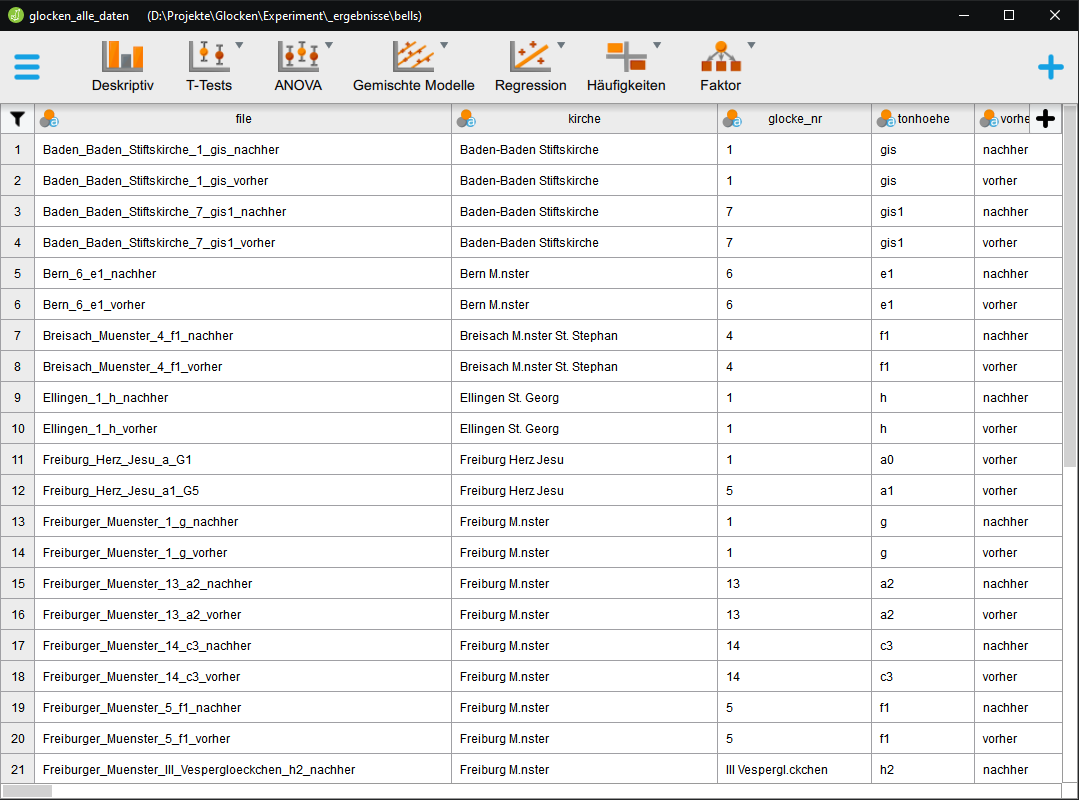
Datentabelle in JASP

Für die statistische Auswertung bzw. zur Prüfung von Signifikanz oder Zusammenhängen können mit einem Klick auf die jeweilige Spalte auch einzelne Datengruppen aus der Auswahl herausgenommen oder hinzugefügt werden.

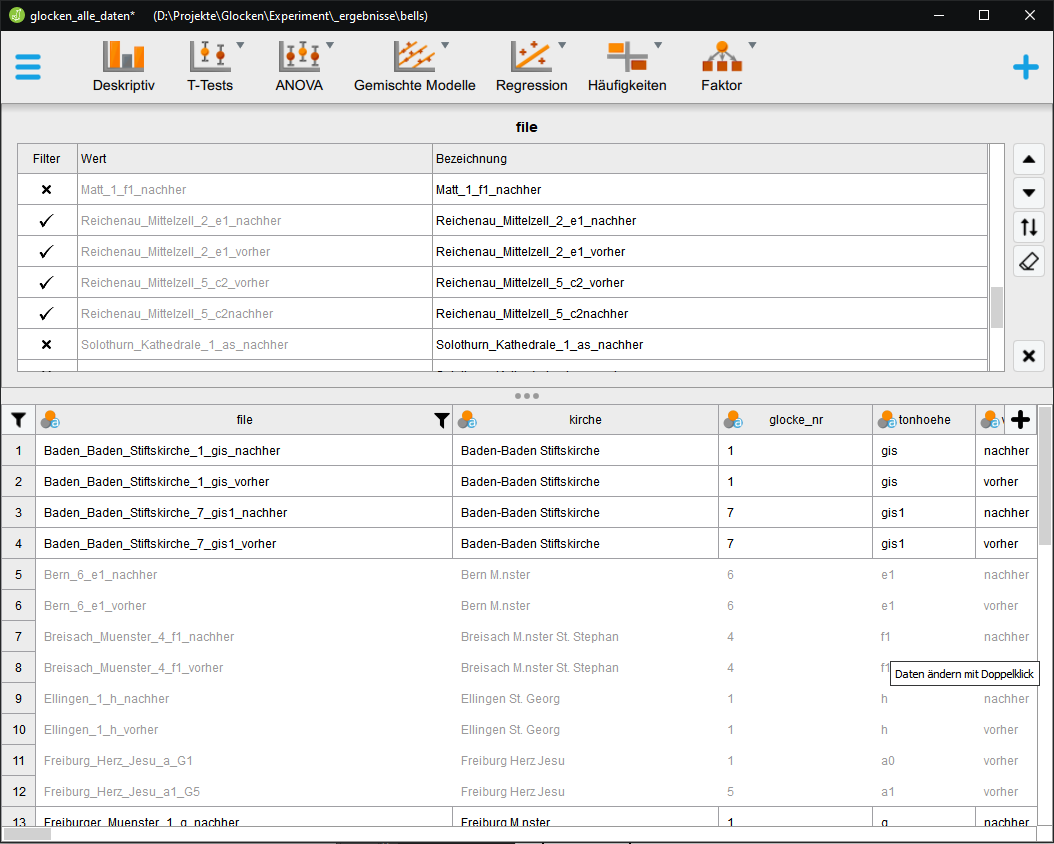
Datenauseahl in JASP, wenn z.B. nur die Daten bestimmter Kirchenglocken ausgewählt werden soll

In den folgenden über das Menü erreichbaren Fenstern sind auf der linken Seite immer alle Variablen (= Spalten einer Tabelle) angeordnet, aus denen man dann die zu überprüfenden Variablen in die rechten jeweiligen Auswahlfenster ziehen kann.

Deskriptive Statistik
(Menü: Deskriptiv)

Im Bereich der deskriptiven Statistik können die Daten nach Variablen geordnet ausgewertet werden sowie in Boxplot-, Violin- und Jitterelementen dargestellt werden.

Weitere Darstellungsarten sind Verteilungs-, Korrelations- und Intervalldiagramme sowie auch die üblichen statistischen Beschreibungsmöglichkeiten wie Modus (am häufigsten vorkommender Wert), Median (Wert, bei dem alle Werte in zwei gleich große Hälften geteilt werden), Mittelwert (Summe aller Werte dividiert durch die Anzahl aller Werte), Standardabweichung (durchschnittliche Abweichung aller Werte vom Mittelwert), Varianz (Quadrat der Standardabweichung) etc.

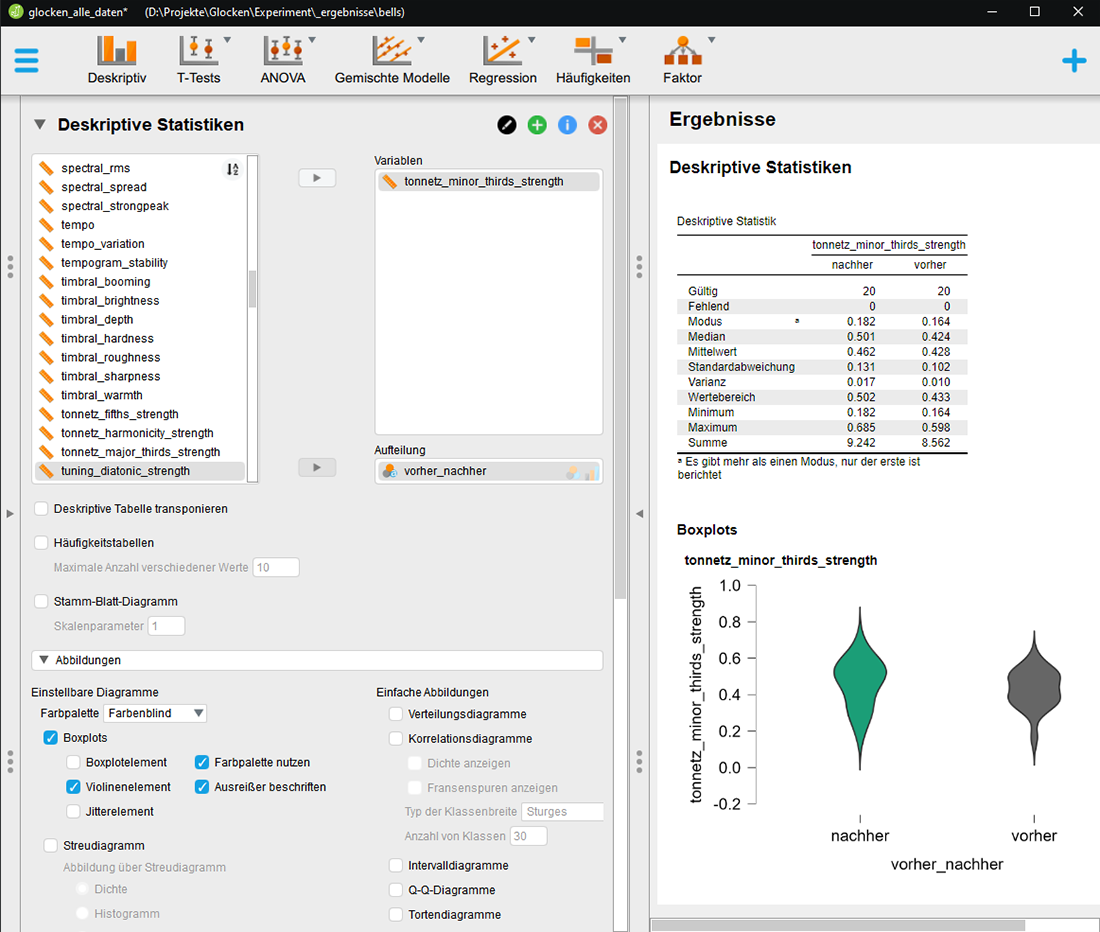
Deskriptive Statistik zur Ausgeprägtheit der Mollterz in Glocken vor und nach einer Restaurierung

t-Test
(ist der Unterschied zwischen zwei Gruppen signifikant oder nicht?)
(Menü: T-Tests -> T-Test für unabhängige Stichproben)

Um die Unterschiede zwischen zwei Gruppen zu prüfen, eignet sich der t-Test, bei dem man die Unterschiede einer oder mehrerer Variablen zwischen zwei Gruppen auf Signifikanz prüfen kann.
Für ein signifikantes Ergebnis muss die Zufallswahrscheinlichkeit p < 0,05 sein, während t die Stärke des Unterschieds angibt (je höher desto stärker) und Cohens d die Effektstärke (kleiner Effekt: d= 0,2-0,5 - mittlerer Effekt: d = 0,5-0,8 - großer Effekt: d>0,8).

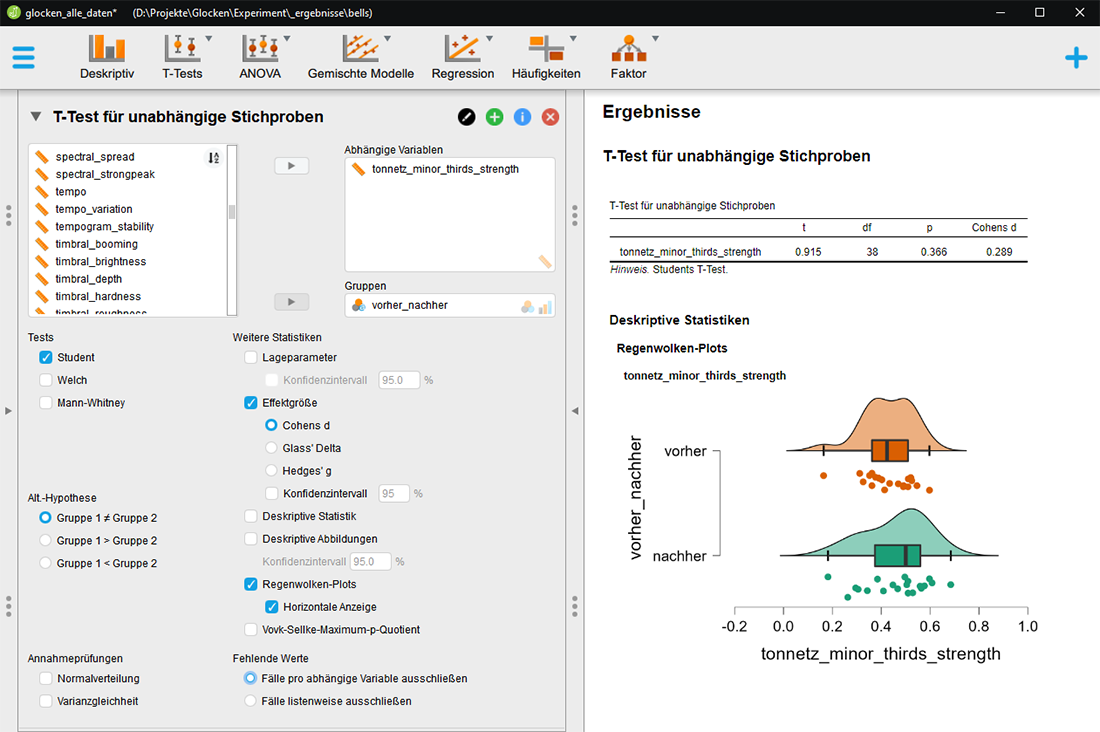
t-Test zur Signifikanz der Anwesenheit einer kleinen Terz im Klangspektrum zur Unterscheidung von originalen und restaurierten Glocken. Mit p von 0,366 ist der Unterschied nicht signifikant und die Effektstärke wäre eher gering = die Ausgeprägtheit einer kleinen Terz kann hier nicht als Kriterium für den Unterschied zwischen originalen und restaurierten Glocken herangezogen werden.

Unter den Punkten "Deskriptive Abbildungen" und "Regenwolken-Plots" gibt es entsprechende Visualisierungsmöglichkeiten.

ANOVA (Analysis of Variance, Varianzanalyse)
(ist der Unterschied zwischen mehr als zwei Gruppen signifikant oder nicht?)
(Menü: ANOVA -> ANOVA)

Um die auf eine Variable zurückführbaren Unterschiede zwischen mehr als zwei Gruppen zu prüfen, eignet sich die Varianzanalyse (ANOVA), bei der man die Unterschiede einer Variablen zwischen mehreren Gruppen auf Signifikanz prüfen kann.
Für ein signifikantes Ergebnis muss die Zufallswahrscheinlichkeit p < 0,05 sein, während F die Stärke des Unterschieds angibt (je höher desto stärker) und η² die Effektstärke (kleiner Effekt: η²= 0,1-0,25 - mittlerer Effekt: η² = 0,25-0,37 - großer Effekt: η²>0,37).

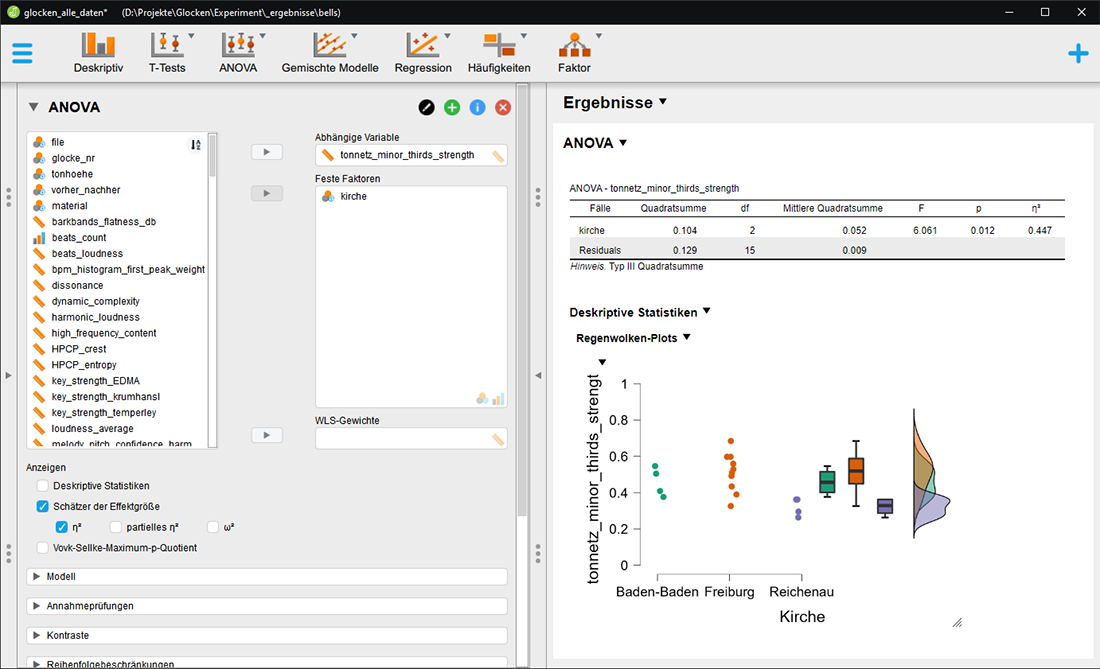
ANOVA zur Signifikanz der Anwesenheit einer kleinen Terz im Klangspektrum zur Unterscheidung von Glocken verschiedener Kirchen. Mit p von 0,012 ist der Unterschied signifikant und die Effektstärke ist mit η² von 0,447 auch sehr groß. Die Ausgeprägtheit einer kleinen Terz kann hier als Kriterium für den Unterschied zwischen den Kirchenglocken in Baden-Baden, Freiburg und Reichenau herangezogen werden.

Unter dem Reiter "Deskriptive Abbildungen" und "Regenwolken-Plots" gibt es entsprechende Visualisierungsmöglichkeiten.

MANOVA (Multivariate Analysis of Variance, Multivariate Varianzanalyse)
(ist der Unterschied zwischen mehr als zwei Gruppen in Abhängigkeit von mehreren Variablen signifikant oder nicht?)
(Menü: ANOVA -> MANOVA)

Um die auf mehrere Variablen zurückführbaren Unterschiede zwischen mehr als zwei Gruppen zu prüfen, eignet sich die Multivariate Varianzanalyse (MANOVA), bei der man die Unterschiede mehrerer Variablen zwischen mehreren Gruppen auf Signifikanz prüfen kann.
Für ein signifikantes Ergebnis muss die Zufallswahrscheinlichkeit p < 0,05 sein, während (Approx.) F die (angenommene) Stärke des Unterschieds angibt (je höher desto stärker).

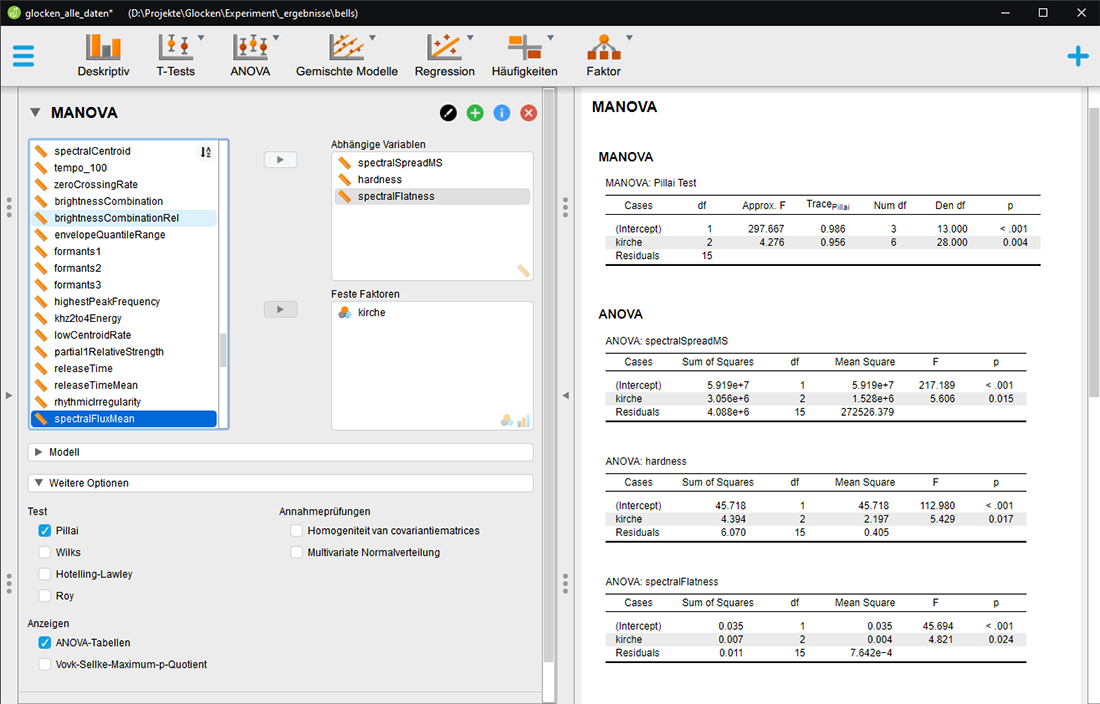
MANOVA zur Signifikanz der spektralen Verteilung, der musikalischen Härte und der spektralen Flachheit zur Unterscheidung von Glocken verschiedener Kirchen. Mit p von 0,004 ist der Unterschied hoch signifikant und auch die ANOVAS über die einzelnen Variablen zeigen signifikante Werte. Anhand von F lässt sich zeigen, dass Härte und Spektrale Verteilung mehr zum Unterschied beitragen als die Spektrale Flachheit.

Über den Punkt "ANOVA-Tabellen" lassen sich für die einzelnen Variablen die entsprechenden ANOVA-Tabellen zeigen, so dass man anhand dieser den Anteil der Variablen für die Unterschiede zwischen den Gruppen einschätzen kann. Die Residuals zeigen hier die Abweichung der durch dieses Modell vorhergesagten Werte gegenüber den tatsächlich beobachteten Werten. Es ist das Ziel, die Residuen möglichst klein zu halten.

Korrelationen
(gibt es einen signifikanten Zusammenhang zwischen den erhobenen Daten und in welche Richtung geht dieser?)
(Menü: Regression -> Korrelation)

Um einen Zusammenhang zwischen mehreren Variablen auf ihre Signifikanz zu prüfen, eignet sich die Korrelation.
Für ein signifikantes Ergebnis muss die Zufallswahrscheinlichkeit p < 0,05 sein, während Pearsons r die Stärke des Unterschieds angibt (je höher desto stärker).

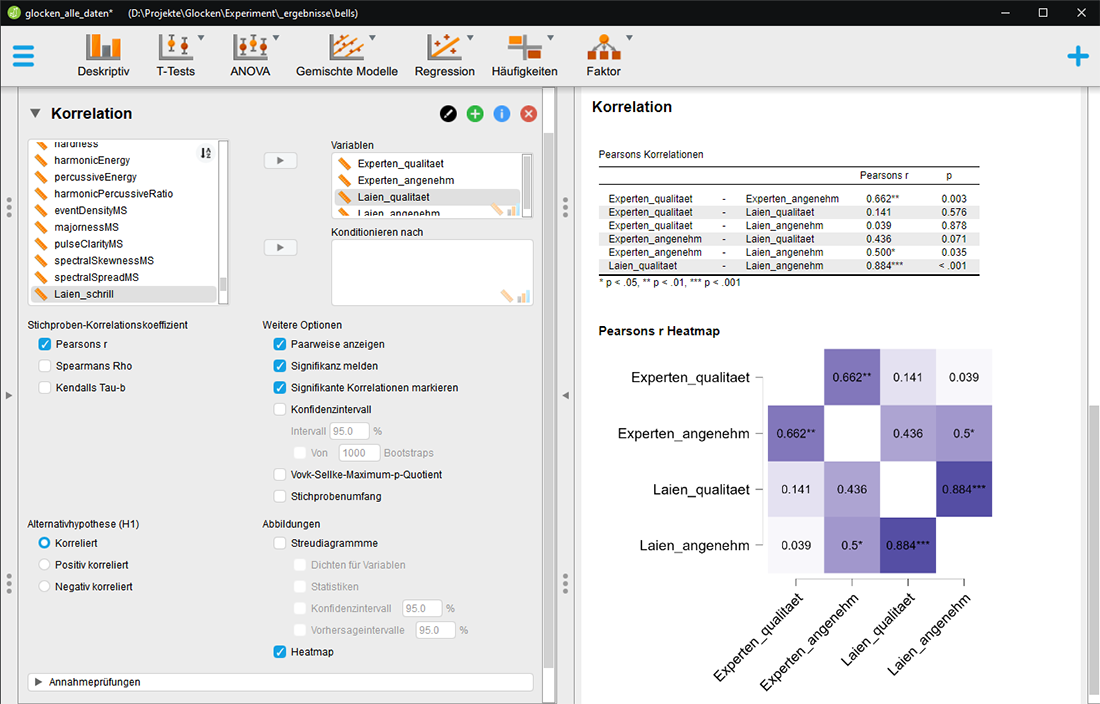
Korrelationsanalyse zu etwaigen Zusammenhängen zwischen Experten- und Laienansichten über die Angenehmheit und die Qualität von Glockenklängen. Es wird deutlich, dass sowohl Experten (r=0,662**) als auch Laien (0,884***) als qualitativ hochwertig empfundene Glocken auch als angenehm empfinden, jedoch scheint es bei der Einschätzung der Qualität keine Übereinstimmung zwischen Laien und Experten zu geben, während bei der Beurteilung der Angenehmheit schon eine gewisse übereinstimmung (r=0,5*) herrscht.(***= höchst signifikant (p<0,001), **= hoch signifikant (p<0,01), *= signifikant (p<0,05)).

Unter dem Punkt "Abbildungen" lassen sich die gefundenen Korrelationen in Streudiagrammen und Heatmaps abbilden.

G*Power - Wie viele Versuchspersonen brauche ich?

Power = Stärke bzw. Güte eines statistischen Tests (statistical power) = Wahrscheinlichkeit für eine Hypothese eine statistische Signifikanz zu finden.

Mit G*Power für Mac und Windows ist es seit 1992 möglich die Anzahl der benötigten Versuchspersonen oder die Effektstärke u.ä. vor einer Studie zu berechnen.

- Mac (https://www.psychologie.hhu.de/fileadmin/redaktion/Fakultaeten/Mathematisch-Naturwissenschaftliche_Fakultaet/Psychologie/AAP/gpower/GPowerMac_3.1.9.6.zip)
- Windows (https://www.psychologie.hhu.de/fileadmin/redaktion/Fakultaeten/Mathematisch-Naturwissenschaftliche_Fakultaet/Psychologie/AAP/gpower/GPowerWin_3.1.9.7.zip)

In der Systematischen Musikwissenschaft gibt es in den meisten Fällen folgende Studiendesigns:

t-Test
(ist der Unterschied zwischen zwei Gruppen signifikant oder nicht?)

Soll ein Unterschied zwischen zwei Gruppen untersucht werden, so wählt man unter Test family "t-Test" aus. Sollen zwei gleichartige/-große Gruppen untersucht werden, dann wählt man unter Statistical Test "Means: Differences between two dependent means (matched pairs)". Sind die Gruppen unterschiedlich/unterschiedlich groß, so wählt man dort "Means: Differences between two independent means (two groups)". Unter Type of power analysis wählt man "A priori: Computer required sample size - given α, power and effect size".

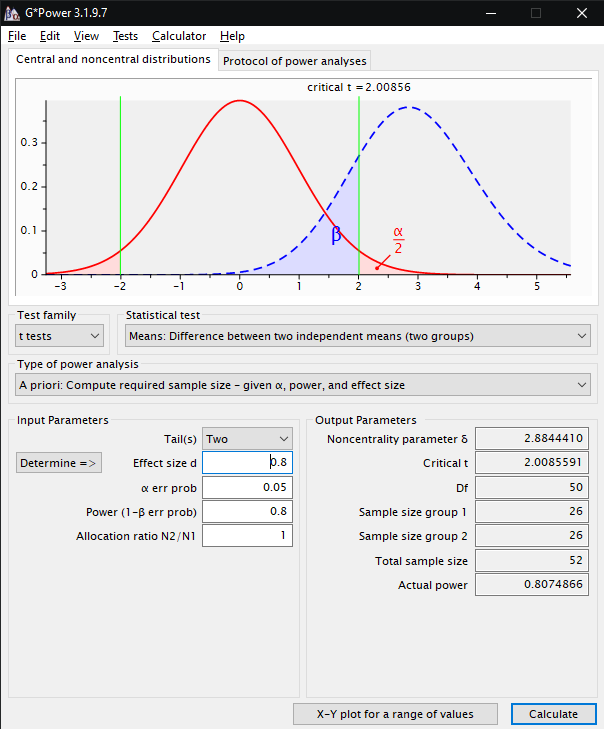
Typische Einstellungen für die Ermittlung der Versuchspersonenanzahl (Sample size group 1 und Sample size group 2)
bei der Ermittlung eines Unterschieds zwischen zwei Gruppen mit großer Effektstärke

Bei den Input Parameters stellt man unter Tail(s) die Anzahl der Richtungen ein: Ist die Richtung des gesuchten Unterschieds schon bekannt (positiv oder negativ), dann ist es "One" Tail. Wenn die Richtung des gesuchten Unterschieds nicht bekannt ist (positiv und negativ), dann sind es "Two" Tails.

Unter Effect Size d kann die voraussichtliche Effektstärke (d) zwischen 0 und 1 eingestellt werden (kleiner Effekt: d= 0,2-0,5 - mittlerer Effekt: d = 0,5-0,8 - großer Effekt: d>0,8).

Bei α err prob wird die Zufallswahrscheinlichkeit eingestellt (signifikant, wenn p<0,05) und bei Power (1-β err prob) der Betafehler (Defaultwert: 0,95, kann aber auch, da er nicht so gravierend ist wie der α-Fehler, bei 0,8 eingestellt werden).

α-Fehler: Nullhypothese wird fälschlicherweise verworfen (z.B. Corona trotz negativem PCR-Test)
β-Fehler: Nullhypothese wird fälschlicherweise beibehalten (z.B. kein Corona trotz positivem PCR-Test)

Unter Allocation ratio N2/N1 kann das Verhältnis der Gruppengrößen in einer Zahl eingetragen werden.

Wenn man auf Calculate klickt, wird unter Sample size group 1 und Sample size group 2 die Anzahl der benötigten Versuchspersonen pro Gruppe angezeigt.

ANOVA (Analysis of Variance, Varianzanalyse)
(ist der Unterschied zwischen mehr als zwei Gruppen signifikant oder nicht?)

Soll ein Unterschied zwischen drei oder mehr Gruppen untersucht werden, so wählt man unter Test family "F-Test" aus, unter Statistical Test "ANOVA: Fixed effects, omnibus, one-way" und unter Type of power analysis "A priori: Computer required sample size - given α, power and effect size".

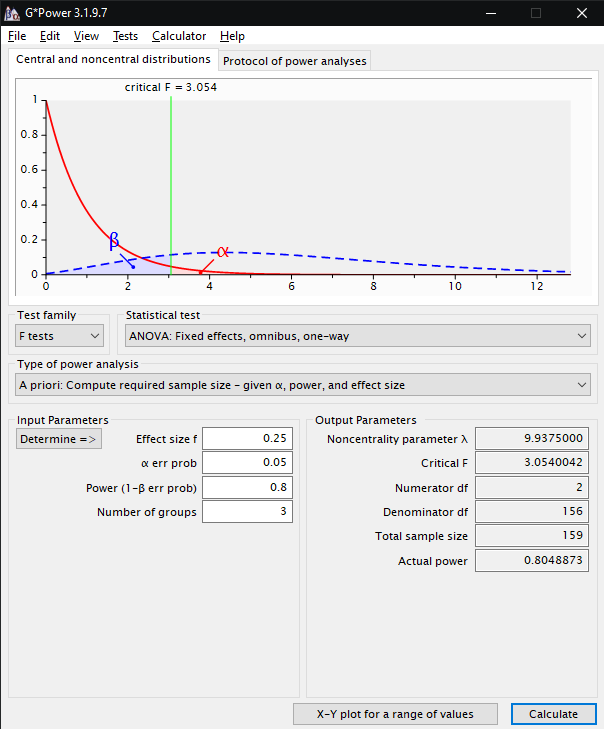
Typische Einstellungen für die Ermittlung der Versuchspersonenanzahl (Total sample size)
bei der Ermittlung von Unterschieden zwischen drei Gruppen mit mittlerer Effektstärke

Bei den Input Parameters stellt man unter Effect Size f die voraussichtliche Effektstärke (f) zwischen 0 und 1 ein (kleiner Effekt: f= 0,1-0,25 - mittlerer Effekt: f = 0,25-0,4 - großer Effekt: f>0,4).

Unter Number of groups wird die Anzahl der zu vergleichenden Gruppen eingegeben.

Wenn man auf Calculate klickt, wird unter Total sample size die Anzahl der benötigten Versuchspersonen angezeigt.

MANOVA (Multivariate Analysis of Variance, Multivariate Varianzanalyse)
(ist der Unterschied zwischen mehr als zwei Gruppen in Abhängigkeit von mehreren Variablen signifikant oder nicht?)

Soll ein auf mehrere Variablen zurückführbarer Unterschied zwischen drei oder mehr Gruppen untersucht werden, so wählt man unter Test family "F-Test" aus, unter Statistical Test "MANOVA: Global effects," und unter Type of power analysis "A priori: Computer required sample size - given α, power and effect size".

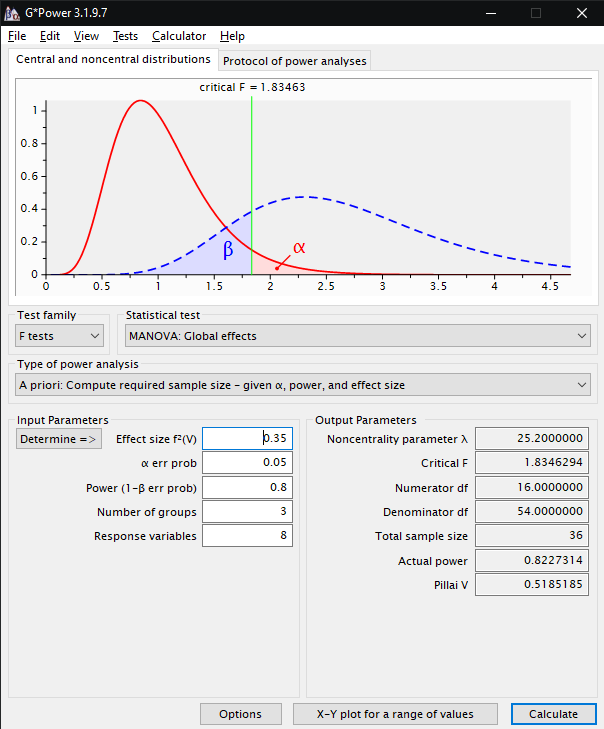
Typische Einstellungen für die Ermittlung der Versuchspersonenanzahl (Total sample size)
bei der Ermittlung von auf mehrere Variablen zurückzuführende Unterschieden zwischen drei Gruppen mit großer Effektstärke

Bei den Input Parameters stellt man unter Effect Size f²(V) die voraussichtliche Effektstärke (f²) zwischen 0 und 1 ein (kleiner Effekt: f²= 0,02-0,15 - mittlerer Effekt: f² = 0,15-0,35 - großer Effekt: f²>0,35).

Unter Number of groups wird die Anzahl der zu vergleichenden Gruppen eingegeben.

Bei Response variables kann die Anzahl der zu erwartenden Variablen eingegeben werden, auf die der Unterschied zurückgeführt werden kann.

Wenn man auf Calculate klickt, wird unter Total sample size die Anzahl der benötigten Versuchspersonen angezeigt.

Korrelationen
(gibt es einen signifikanten Zusammenhang zwischen den erhobenen Daten und in welche Richtung geht dieser?)

Sollen Korrelationen untersucht werden, so wählt man unter Test family "Exact" aus, unter Statistical Test "Correlation: Bivariate normal model" und unter Type of power analysis
"A priori: Computer required sample size - given α, power and effect size".

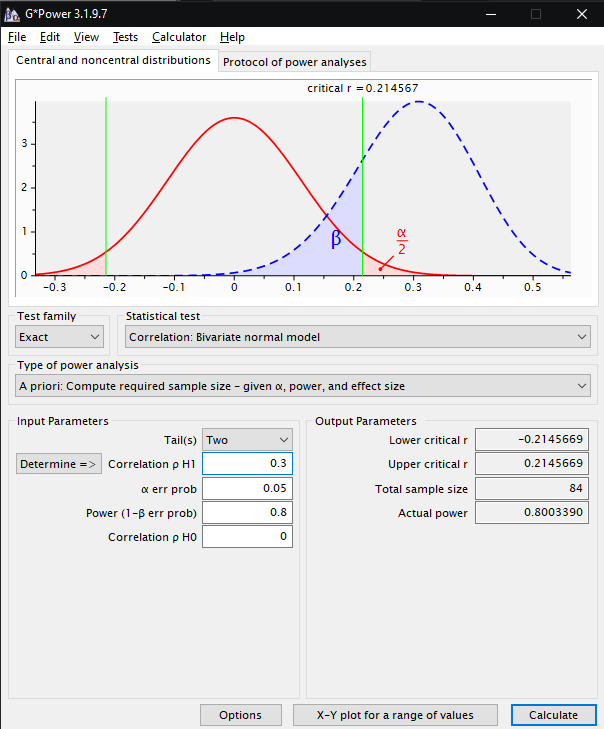
Einstellungen für die Ermittlung der Versuchspersonenanzahl (Total sample size)
bei einer Suche nach Korrelationen mit kleiner Effektstärke

Bei den Input Parameters stellt man unter Tail(s) die Anzahl der Richtungen ein: Ist die Richtung der gesuchten Korrelation schon bekannt (positiv oder negativ), dann ist es "One" Tail. Wenn die Richtung der gesuchten Korrelation nicht bekannt ist (positiv und negativ), dann sind es "Two" Tails.

Unter Correlation ρ H1 kann die voraussichtliche Effektstärke (r) zwischen 0 und 1 eingestellt werden (kleiner Effekt: r<= 0,3 - mittlerer Effekt: r = 0,3-0,5 - großer Effekt: r>0,5)

Wenn man auf Calculate klickt, wird unter Total sample size die Anzahl der benötigten Versuchspersonen angezeigt.