Signalanalyse und Music Information Retrieval (MIR)
Seit ca. 2000 lassen sich dank Signalanalyse-Techniken klangliche Eigenschaften wie Helligkeit oder Rauhigkeit direkt aus Wavedateien auslesen.
Gängige Toolboxen oder Libraries sind hier z.B.
•
Essentia (Python)
• Librosa (Python)
• Timbre Toolbox (MatLab)
• MIRToolbox (MatLab)
Diese Libraries sind sehr nützlich, wenn es um die Suche nach klanglicher Ähnlichkeit von Musik, Klängen oder Stimmen geht, um Musik-Empfehlungssysteme, automatische Genre-Klassifikationen und um viele andere klang-/musikbezogene Aufgaben.
Typische Timbre Features / Deskriptoren:
- Brightness:
Anteil der spektralen Energie (in %) oberhalb von 1500 Hz
-> je höher desto heller der Klang - ZeroCrossingRate:
Häufigkeit des Nulldurchgangs einer Schwingung pro Zeiteinheit
-> je höher desto geräuschhafter/heller der Klang - HarmonicEnergy:
Energieanteil der horizontalen Linien im Sonagramm
-> je höher desto mehr stationäre Anteile sind im Spektrum. - PercussiveEnergy:
Energieanteil der vertikalen Linien im Sonagramm
-> je höher desto mehr perkussive Anteile sind im Spektrum - Inharmonicity:
Anteil des Spektrums, der nicht in einem ganzzahlig vielfachen Verhältnis zum Grundton steht
-> je höher desto inharmonischer - TonalEnergy:
Anteil des Spektrums, der in einem ganzzahlig vielfachen Verhältnis zum Grundton steht
-> je höher desto tonaler - SpectralCentroid:
Geometrischer Schwerpunkt des Spektrums
-> korreliert mit Helligkeit, je höher desto heller der Klang - SpectralFlatness:
Spektrale "Flachheit"
-> je höher, desto weniger Peaks sind im Spektrum - SpectralFlux:
Spektrale Änderung von Frame zu Frame
-> je höher desto mehr spektrale Änderungen in der Zeit (z.B. bei Sprache) - SpectralEntropy:
Anteil einer statistischen Verteilung von Frequenzen im Spektrum
-> je höher desto flacher das Spektrum (Rauschen = 1), je geringer desto mehr wird das Spektrum von einzelnen Teiltönen dominiert (0 = Sinuston) - EventDensity:
Anzahl der Onsets pro Sekunde
-> wie viele Töne pro Sekunde gespielt werden (ähnlich: tempoOnsets)
Matlab mit MIR-Toolbox
MatLab
(ab Ende der 1970er Jahre; seit 1984 kommerziell, MathWorks,
Cleve
Moler, Jack Little, Steve Bangert)
Matrizen-Labor, für Datenanalyse/Auswertung und Simulation, meist auf der Grundlage von Matrizen. Für Audio-Dateien
MIRtoolbox
(ab 2007, Olivier Lartillot, Petri Toiviainen und Toumas
Eerola)
Toolbox für Music Information Retrieval = Musikalische Merkmale aus Klangdateien extrahieren und miteinander vergleichen.
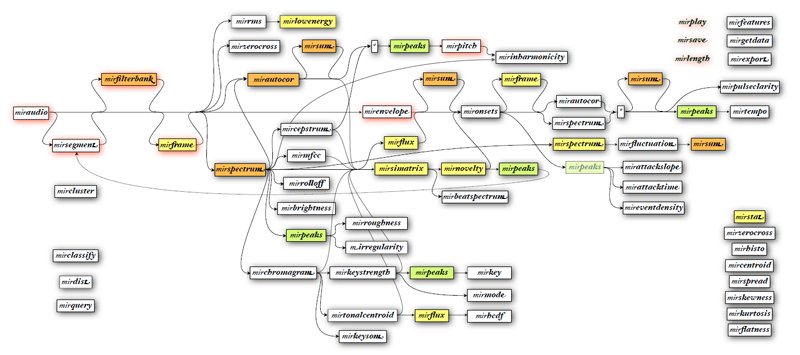
Möglichkeiten der MIRToolbox
(Usermanual MIRToolbox)
Dateien einladen via miraudio():
miraudio('klangdatei')
lädt
eine Klangdatei mit dem Namen "Klangdatei" und der Endung "wav",
"au", "aiff" oder "mp3" aus dem aktuellen
Verzeichnis und stellt die Wellenform dar.
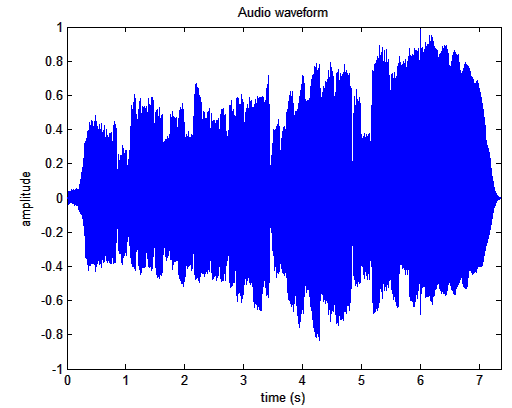
Darstellung einer Tonleiter einer Bassklarinette als Wellenform
miraudio('klangdatei',
'Sampling', 11025)
lädt
eine Klangdatei mit dem Namen "Klangdatei" und mit einer Sample-Rate
von 11025 Hz ein
miraudio('klangdatei',
'Channel', 1)
lädt
den linken Kanal einer Klangdatei mit dem Namen "Klangdatei"
ein
miraudio('klangdatei',
'Trim')
entfernt
beim Einladen automatisch Stille am Anfang und Ender der Datei.
miraudio('klangdatei',
'Extract', 2,3,'s','Start')
Extrahiert einen Ausschnitt
aus der Datei (hier: von der 2. zur 3. Sekunde ab Beginn des Samples)
miraudio('Folder')
lädt
alle Klangdateien innerhalb eines Ordners ein
miraudio('Folders')
lädt
alle Klangdateien innerhalb eines Ordners inklusive der Unterordner ein
klangvariable = miraudio('klangdatei')
Die
eingeladene Klangdatei wird einer Variablen (klangvariable) zugewiesen.
Spektrum darstellen mit mirspectrum ():
mirspectrum('klangdatei')
oder mirspectrum(klangvariable)
es wird das Spektrum
der eingeladenen Datei oder der damit verbundenen Variablen dargestellt.
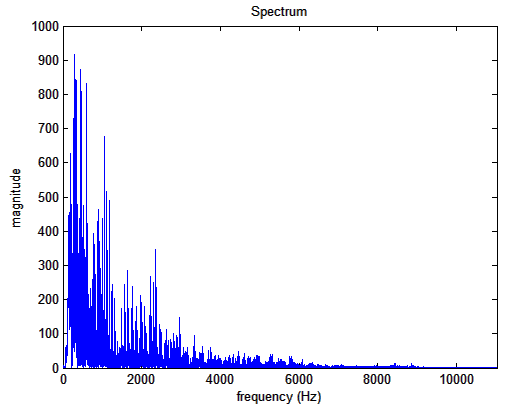
Darstellung
einer Tonleiter einer Bassklarinette als Spektrum
mirspectrum('klangdatei','Min',
50, 'Max', 5000)
mit 'Min'
und 'Max' lassen sich die Grenzen des Spektrums einstellen
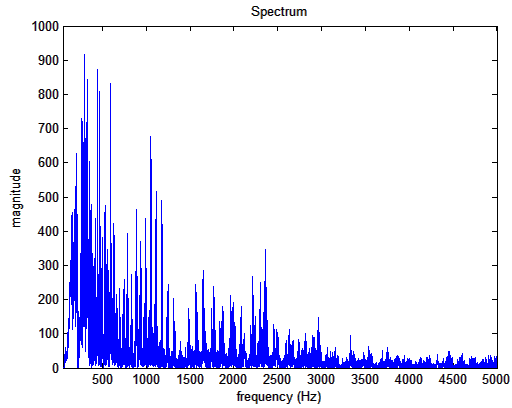
Darstellung einer Tonleiter einer Bassklarinette als Spektrum zwischen
50 und 5000 Hz
mirspectrum('klangdatei','Frame','Min',
50, 'Max', 5000)
mit 'Frame' wird anstelle
eines Spektrums ein Sonagramm dargestellt.
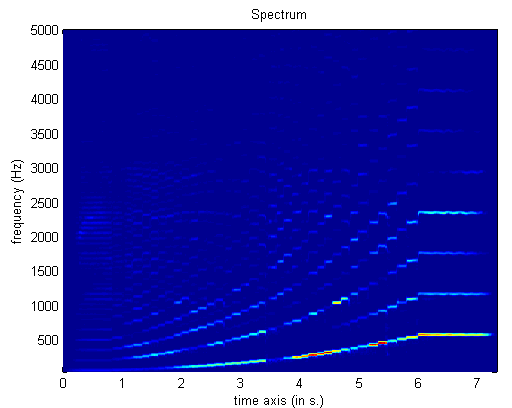
Darstellung
einer Tonleiter einer Bassklarinette als Sonagramm zwischen 50 und 5000
Hz
(Zeitfensterlänge ist standardmäßig bei 50 ms, Fenster
ist standardmäßig Hamming)
mirspectrum('klangdatei','Frame','Min',
50, 'Max', 5000, 'Normal')
mit 'Normal' wird das
Spektrum/Sonagramm vor der Darstellung normalisiert.
mirspectrum('klangdatei','Min',
50, 'Max', 5000, 'Normal', 'dB')
mit 'dB' erfolgt die
Ausgabe der Amplitudenwerte als Dezibel-Werte.
mirspectrum('klangdatei','Min',
50, 'Max', 5000, 'Frame', 'Mel')
mit 'mel' erfolgt die
Ausgabe der Frequenzwerte als Mel-Werte.
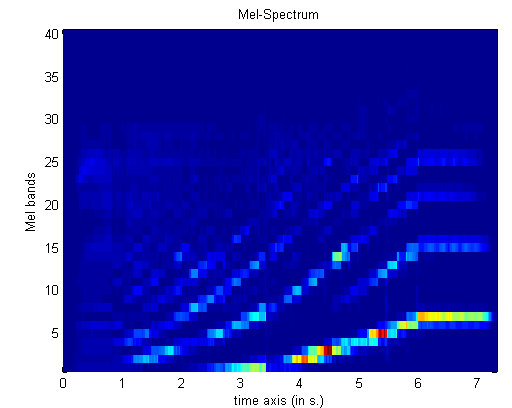
Darstellung einer Tonleiter einer Bassklarinette als Sonagramm zwischen
50 und 5000 Hz als Mel-Werte
mirspectrum('klangdatei','Min',
50, 'Max', 5000, 'Frame', 'Cents')
mit 'Cents' erfolgt
die Ausgabe der Frequenzwerte als Cents-Werte bezogen auf MIDI-Werte,
d.h. die MIDI-Tonhöhe wird mit 100 multipliziert, z.B. a' hat 440
Hz und die MIDI-Note 69. in MIDI-Cents sind es 69*100=6900.
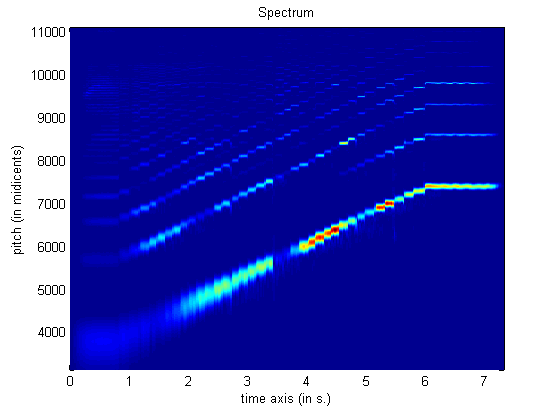
Darstellung
einer Tonleiter einer Bassklarinette als Sonagramm zwischen 50 und 5000
Hz als Cents-Werte
Spitzen im Spektrum (oder in anderen Kurven) finden via Peak Picking
Mit mirpeaks() lassen sich Spitzenwerte im Spektrum finden (im Spektrum als rote Kreise angezeigt und im Sonagramm als weisse oder schwarze Kreuze). Über 'Contrast' und 'Treshold' kann die Genauigkeit der Ergebnisse bestimmt werden:
a=mirspectrum('klangdatei','Frame','Min', 50, 'Max', 5000) ; mirpeaks(a,'Contrast',0.5,'Threshold',0.2)
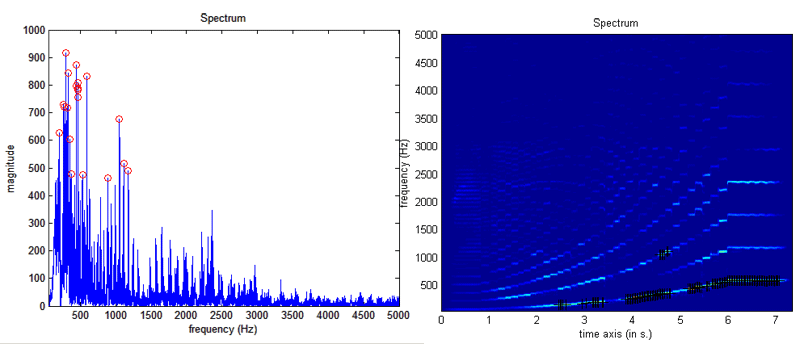
Darstellung einer Tonleiter einer Bassklarinette als Spektrogramm
und Sonagramm mit Peaks
Über den Zusatz 'Only' werden nur die Peaks dargestellt. mit 'Track' (und einer Zeit (in ms) dahinter, z.B. 'Track', 25) lassen sich die Peaks in Sonagrammen tracken.
Hüllkurve darstellen mit mirenvelope
Mit mirenvelope() kann die Amplitudenhüllkurve eines Klangsignals dargestellt werden:
mirenvelope('klangdatei')
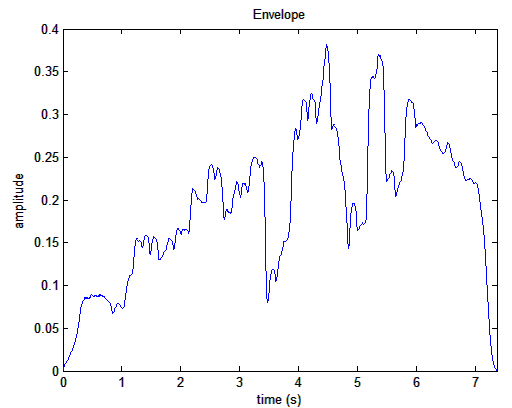
Darstellung
einer Tonleiter einer Bassklarinette als Amplitudenhüllkurve
Bandpassfiltern mit mirfilterbank
Mit mirfilterbank() kann man den Klang spektral in einzelne Frequenzabschnitte unterteilen. Dies kann zum einen in der Standardeinstellung als gammatone-Filterbank geschehen:
mirfilterbank('klangdatei')
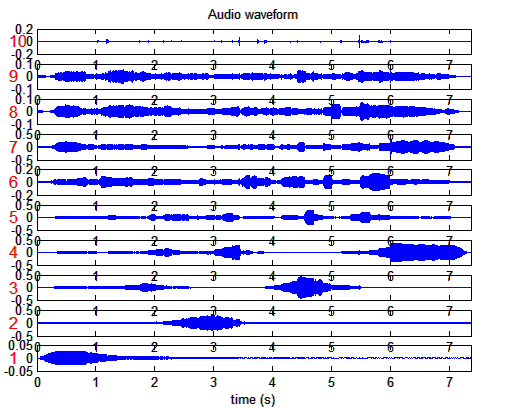
Darstellung
einer Tonleiter einer Bassklarinette auf 10 Frequenzbereiche aufgeteilt
Zum anderen kann dies auch mit spezifischen Einstellungen geschehen, wie z.B. abgestimmt auf die im Klang vorkommenden Grundfrequenzen, z.B. auf harmonische Klänge mit einem Grundton von 75 Hz:
mirfilterbank('klangdatei', 'Manual', [-Inf, 75, 150, 225, 300, 375, 450, 525, 600, 675, 750, 825, 900, Inf])
Mit 'Manual' wird gesagt, dass die Filterbänder manuell eingestellt werden und in den eckigen Klammern (Zeilenvektor) dahinter werden die einzelnen Mittenfrequenzen eingegeben (wobei -Inf am Anfang ein Tiefpassfilter und Inf am Ende ein Hochpassfilter bedeutet)
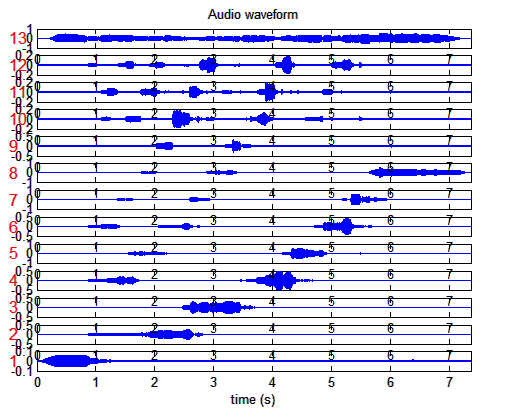
Darstellung
einer Tonleiter einer Bassklarinette auf 13 eher passendere Frequenzbereiche
aufgeteilt
Von diesen einzelnen Kanälen lassen sich über mirenvelope() ebenfalls die Amplitudenhüllkurven ermitteln:
a=mirfilterbank('klangdatei', 'Manual', [-Inf, 75, 150, 225, 300, 375, 450, 525, 600, 675, 750, 825, 900, Inf]);mirenvelope(a)
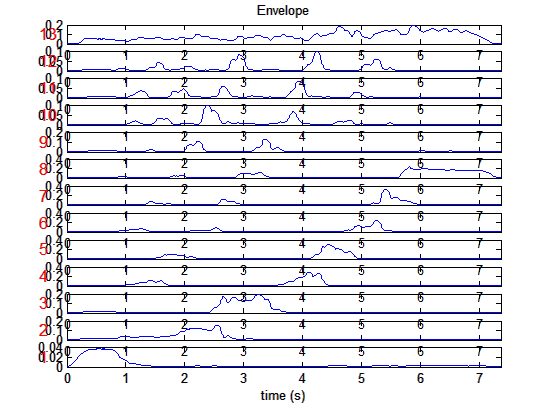
Darstellung
einer Tonleiter einer Bassklarinette auf 13 eher passendere Frequenzbereiche
aufgeteilt in Hüllkurven
Diese Hüllkurven lassen sich (auch nach einer Bearbeitung/Veränderung) über mirsum() wieder zu einer Gesamthüllkurve zusammenfassen:
a=mirfilterbank('klangdatei', 'Manual', [-Inf, 75, 150, 225, 300, 375, 450, 525, 600, 675, 750, 825, 900, Inf]);b=mirenvelope(a);mirsum(b)
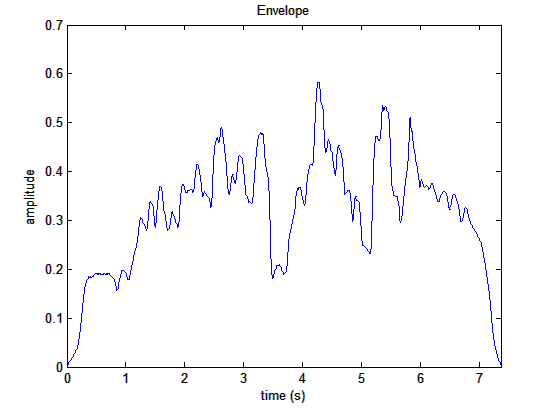
Darstellung einer Tonleiter einer Bassklarinette auf 13 eher passendere
Frequenzbereiche
aufgeteilt in Hüllkurven und Zusammenfassung dieser in einer Hüllkurve
Tonhöhe ermitteln mit mirpitch
Über mirpitch() kann die Grundtonhöhe eines Klanges bestimmt werden:
mirpitch('klangdatei')
bei einer eindeutigen Tonhöhe erhält man eine Meldung wie
The Pitch related to file bassklarinette is 75.364 Hz
bei mehrdeutigen Tonhöhen bekommt man eine Grafik ausgegeben:
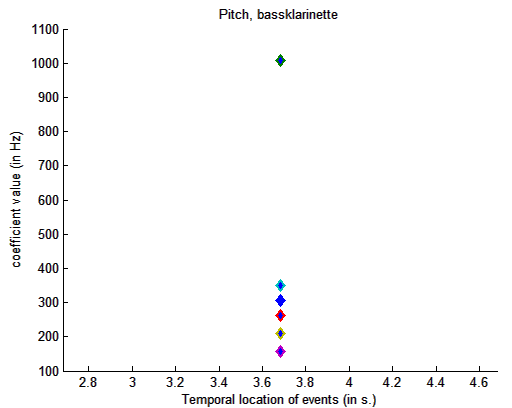
Darstellung
der Tonhöhen einer Tonleiter einer Bassklarinette unabhängig
von der Zeit
Wenn sich die Tonhöhen in der Zeit ändern sollte man deswegen am besten das Attribut 'Frame' hinzufügen:
mirpitch('klangdatei', 'Frame')
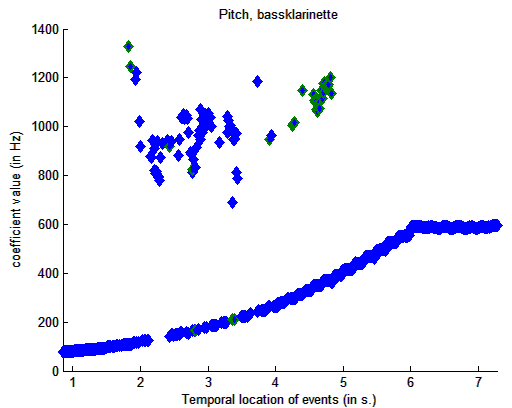
Darstellung
der Tonhöhen einer Tonleiter einer Bassklarinette im zeitlichen Verlauf
(mit Artefakten im oberen Teil der Grafik)
Über a=mirpitch('klangdatei','Frame'); mirplay(a) kann man den Verlauf auch hörbar machen.
Dynamik ermitteln mit mirrms
Über mirrms() lässt sich die Quadratwurzel der Gesamtenergie eines Signals angeben.
mirrms('klangdatei')
Man erhält als Antwort den Gesamtenergiewert (bezogen auf 1)
The RMS energy related to file bassklarinette is 0.25645
Wenn man den Energieverlauf über die Zeit wissen will, kann man auch mit 'Frame' für alle 50 ms einen Quadratwurzelwert sich wiedergeben lassen:
mirrms('klangdatei','Frame')
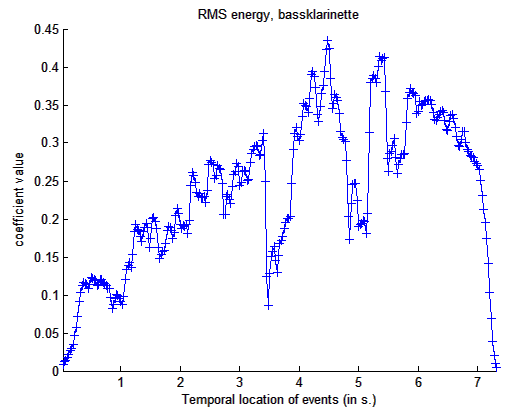
Darstellung
der RMS Energie einer Tonleiter einer Bassklarinette im zeitlichen Verlauf
Spektralen Schwerpunkt ermitteln mit mircentroid
Über mircentroid() kann der Spectral Centroid eines Klanges bestimmt werden:
mircentroid('klangdatei')
man erhält als Ergebnis eine Antwort wie:
The Spectral centroid related to file bassklarinette is 1519.6112 Hz
Wenn man den Verlauf des Spectral Centroids über die Zeit wissen will, kann man auch sich mit 'Frame' für alle 50 ms den dazugehörenden Wert wiedergeben lassen:
mircentroid('klangdatei','Frame')
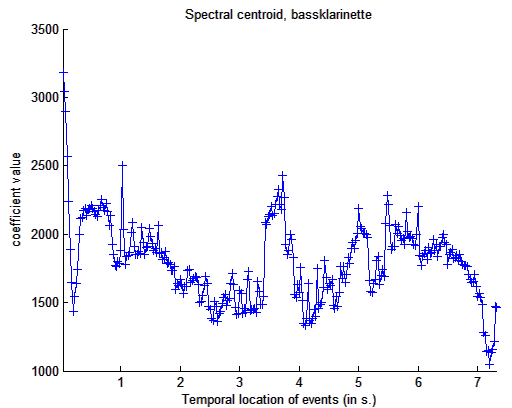
Darstellung
des Spectral Centroids einer Tonleiter einer Bassklarinette im zeitlichen
Verlauf
Über a=mircentroid('klangdatei','Frame'); mirplay(a) kann man den Verlauf auch hörbar machen.
Spektrale Schwankungen (Spectral Flux) ermitteln mit mirflux
Über mirflux() kann der Spectral Flux eines Klanges bestimmt werden:
mirflux('klangdatei')
man erhält als Ergebnis den Fluktuationsverlauf des Klangbeispiels
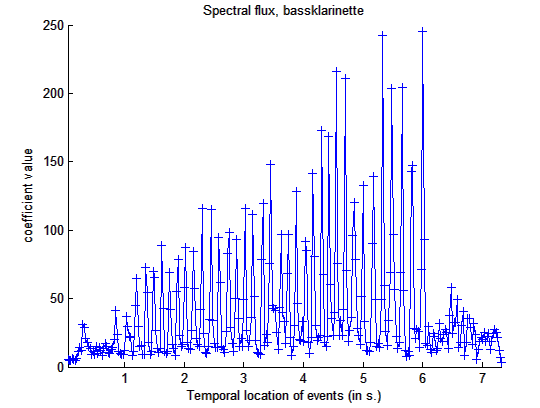
Darstellung
des Spectral Flux einer Tonleiter einer Bassklarinette im zeitlichen Verlauf
Helligkeit ermitteln mit mirbrightness
Über mirbrightness() kann die Helligkeit eines Klanges bestimmt werden:
mirbrightness('klangdatei')
man erhält als Ergebnis eine Antwort wie:
The Brightness related to file bassklarinette is 0.36146
Wenn man den Verlauf der Helligkeit über die Zeit wissen will, kann man auch sich mit 'Frame' für alle 50 ms den dazugehörenden Wert wiedergeben lassen:
mirbrightness('klangdatei','Frame')
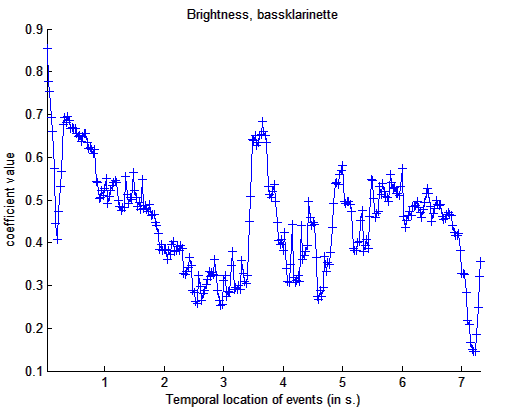
Darstellung
der Helligkeit einer Tonleiter einer Bassklarinette im zeitlichen Verlauf
Inharmonizität ermitteln mit mirinharmonicity
Über mirinharmonicity() kann die Inharmonizität eines Klanges bestimmt werden:
mirinharmonicity('klangdatei')
man erhält als Ergebnis eine Antwort wie:
The Inharmonicity related to file bassklarinette is 0.50307
Wenn man den Verlauf der Inharmonizität über die Zeit wissen will, kann man auch sich mit 'Frame' für alle 50 ms den dazugehörenden Wert wiedergeben lassen:
mirinharmonicity('klangdatei','Frame')
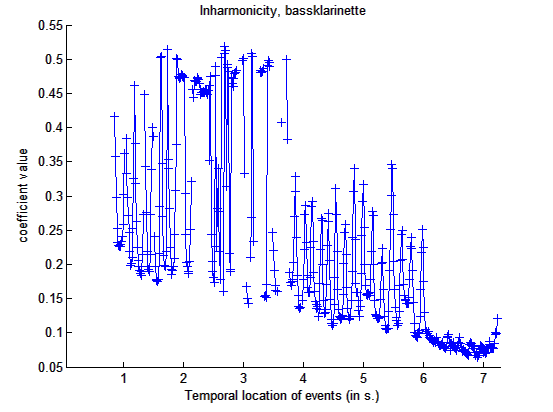
Darstellung
der Inharmonizität einer Tonleiter einer Bassklarinette im zeitlichen
Verlauf
Rauhigkeit ermitteln mit mirroughness
Über mirroughness() kann die Rauhigkeit eines Klanges bestimmt werden:
mirroughness('klangdatei')
man erhält als Ergebnis den Rauhigkeitsverlauf des Klangs
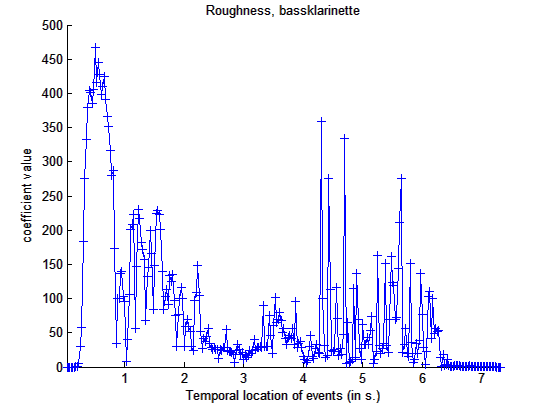
Darstellung
der Rauhigkeit einer Tonleiter einer Bassklarinette im zeitlichen Verlauf
Tempo ermitteln mit mirtempo
Mit mirtempo() kann das Tempo eines Musikstücks bestimmt werden:
mirtempo('klangdatei')
man erhält als Ergebnis eine Antwort wie:
The Tempo related to file bassklarinette is 57.8013 bpm
Wenn man den Tempoverlauf über die Zeit wissen will, kann man auch sich mit 'Frame' für alle 50 ms den dazugehörenden Wert wiedergeben lassen:
mirtempo('klangdatei','Frame')
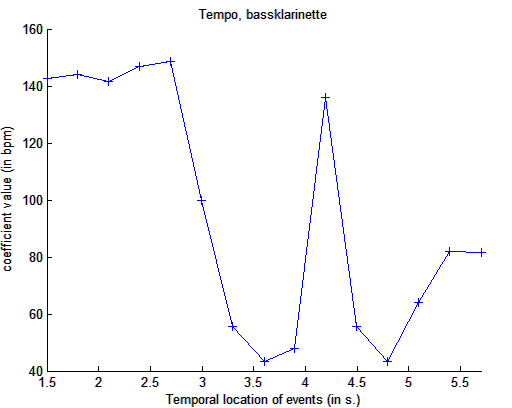
Darstellung
der Tempoverlaufs einer Tonleiter einer Bassklarinette
Tonart ermitteln mit mirtkey
Mit mirkey() kann die Tonart eines Musikstücks bestimmt werden:
mirkey('klangdatei')
man erhält als Ergebnis eine Antwort wie:
The Key related to file bassklarinette is C min
Da die Tonartbestimmung je nach Klangdatei ähnlich unsicher ist wie die Tempobestimmung kann mit mirkeystrength() die Wahrscheinlichkeit einer bestimmten Tonart für das Stück angezeigt werden:
mirkeystrength('klangdatei')
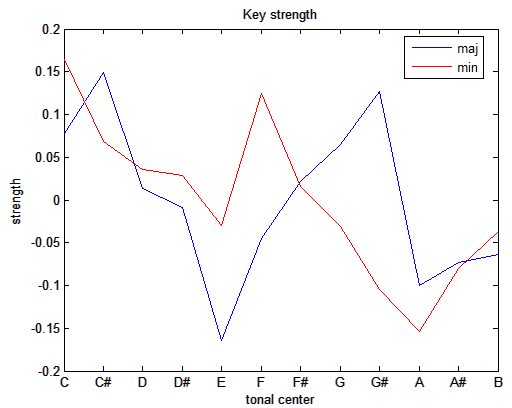
Darstellung
der möglichen Tonarten bei der Tonleiter einer Bassklarinette
Chromagramm ermitteln mit mirchromagram
Über mirchromagram() kann die Verteilung der Tonhöhen über Pitch Classes ermittelt werden:
mirchromagram('klangdatei')
man erhält als Ergebnis eine Grafik mit allen Pitch Classes (bei einer Tonleiter ist es schwierig, da gleich alle Pitch Classes mehr oder weniger gleich abgedeckt werden):
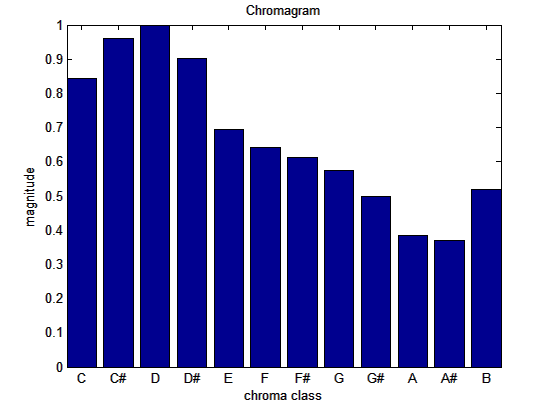
Darstellung
der Pitch Classes bei der Tonleiter einer Bassklarinette
Wenn man den Verlauf der Pitch Classes über die Zeit wissen will, kann man auch sich mit 'Frame' für alle 50 ms den dazugehörenden Wert wiedergeben lassen:
mirchromagram('klangdatei','Frame')
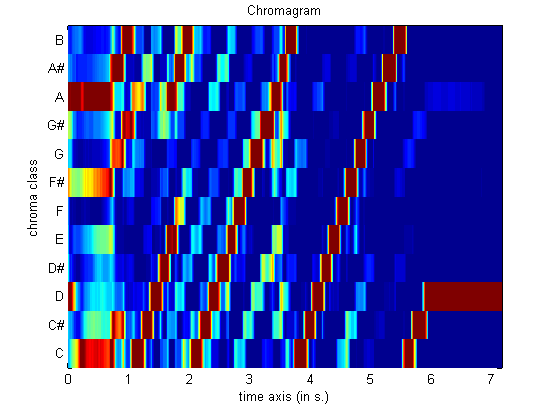
Darstellung der Pitch Classes bei der Tonleiter einer Bassklarinette über
die Zeit
mit dem Zusatz 'Wrap', 'no' kann man sich auch den Verlauf der Tonhöhen über die Zeit wiedergeben lassen:
mirchromagram('klangdatei','Frame', 'Wrap', 'no')
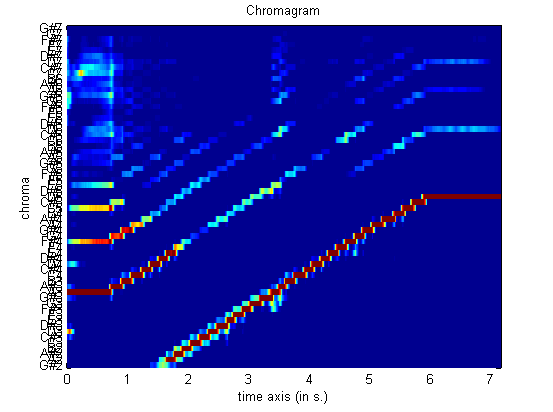
Darstellung
der Tonhöhen bei der Tonleiter einer Bassklarinette über die
Zeit
Dur / Moll erkennen mit mirmode
Über mirmode() kann ermittelt werden, ob das Stück eher in Dur oder Moll steht:
mirmode('klangdatei')
man erhält als Ergebnis eine Antwort wie:
The Mode related to file bassklarinette is -0.015308
Je näher der Wert an +1 ist, desto eher entspricht es einer Durtonart und je mehr der Wert an -1 ist, desto mehr entspricht es einer Molltonart
Wenn man den Verlauf der Dur-Moll-Wahrscheinlichkeit über die Zeit wissen will, kann man auch sich mit 'Frame' für alle 50 ms den dazugehörenden Wert wiedergeben lassen:
mirmode('klangdatei','Frame')
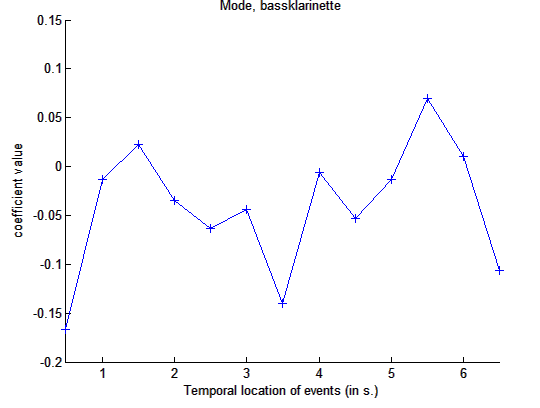
Darstellung
der Dur/Moll-Tonalität bei der Tonleiter einer Bassklarinette über
die Zeit
Toneinsätze erkennen mit mironsets
Über mironsets() können die Einsatzzeitpunkte der einzelnen Töne ermittelt werden, mit dem Zusatz 'Attacks' werden die Einschwingsteigungen gleich mit angegeben:
mironsets('klangdatei','Attacks')
man erhält als Ergebnis den Verlauf der Einsatzzeiten im Stück
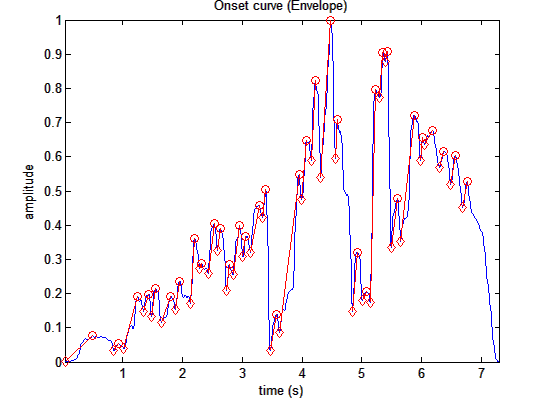
Darstellung
der Einsatzzeiten einer Tonleiter einer Bassklarinette im zeitlichen Verlauf
Mit Hilfe von mirsegment() kann man entlang der Onset-Zeiten das Klangbeispiel in einzelne Segmente unterteilen:
a = mironsets('bassklarinette',
'Attacks')
b = mirsegment('bassklarinette', a)
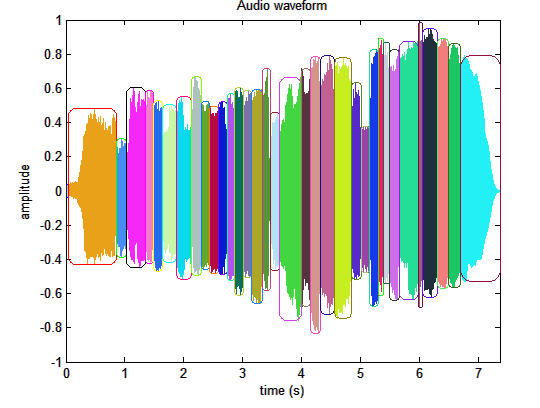
Segmente anhand
Einsatzzeiten einer Tonleiter einer Bassklarinette im zeitlichen Verlauf
Audioausgabe nach bestimmten Kriterien
Mit mirplay('klangdatei') lässt sich eine Klangdatei direkt abspielen (ebenfalls eine damit verbundene Variable mit mirplay('variable')).
Mit dem Zusatz 'Extract', Anfangszeit (sek), Endzeit (sek) kann man auch einen beliebigen Ausschnitt (z.B. von der 3. bis zu 5. Sekunde) aus der Klangdatei spielen:
mirplay('klangdatei', 'Extract', 3,5)
Es gibt auch einen MIR-Toolbox-eigenen Player, den man über mirplayer(variable) starten kann, z.B.:
a = mirbrightness('klangdatei',
'Frame')
mirplayer(a)
Wenn man das Abspielen von Klangdateien auf einen ganzen Ordner bezieht, so kann man die Reihenfolge des Abspielens auch nach klanglichen Aspekten ordnen, wie z.B. nach dem Kriterium von ansteigender Helligkeit:
mirplay('Folder', 'Increasing', mirbrightness('Folder'))
Werte außerhalb der MIR-Toolbox weiterverwenden mit mirgetdata
mit mirgetdata() kann man die Informationen aus MIR-Objekten (z.B. mirfilterbank(x)) als Array in Matlab ablegen und dort weiterverarbeiten (d.h., die Werte werden von ihren Einheiten/Bedeutungen gelöst und liegen als reine Zahlenwerte vor, mit denen man dann weiterrechnen kann):
einzelne_filterbaender
= mirfilterbank('klangdatei');
werte_als_array = mirgetdata(einzelne_filterbaender);
Anwendungsbeispiele:
Vocoder-Script
(Script: Isabella Czedik-Eysenberg 2014)
in der Datei "vocoder.m" folgendes Script schreiben:
function output = vocoder(c, f)
% Synthese-
(carrier) und Analyse-Signal (formant) als miraudio-Objekte
% einlesen:
% Synthesesignal einlesen
carrier = miraudio(c);
% Spektrum des Synthesesignals darstellen
mirspectrum(c, 'Frame', 'Min',
0, 'Max', 2000, 'NormalInput')
% Synthesesignal abspielen
mirplay(c)
% Analysesignal
einlesen
formant = miraudio(f);
% Spektrum des Analysesignals darstellen
mirspectrum(f, 'Frame', 'Min',
0, 'Max', 2000, 'NormalInput')
% Analyesesignal abspielen
mirplay(f)
% Aufteilen beider Signale in Frequenzbänder
% dies
kann manuell geschehen oder auf der Grundlage der
% Voreinstellungen der mirfilterbank:
% manuell:
% bands = [-Inf, 31.5, 35.5, 40, 45, 50, 56, 63, 71, 80, 90, 100, 112,
125, 140, 160, 180, 200, 224, 250, 280, 315, 355, 400, 450, 500, 560,
630, 710, 800, 900, 1000, 1120, 1250, 1400, 1600, 1800, 2000, 2240, 2500,
2800, 3150, 3550, 4000, 4500, 5000, 5600, 6300, 7100, 8000, 9000, 10000,
11200, 12500, Inf];
% cBands = mirfilterbank(carrier, 'Manual', bands);
% cBandsData = mirgetdata(cBands);
% fBands = mirfilterbank(formant, 'Manual', bands);
% mit
Voreinstellungen der mirfilterbank:
% Synthesesignal in Filterbereiche aufteilen
cBands = mirfilterbank(carrier);
% Daten der Synthesefilterbereiche in eine Variable
(cBandsData) speichern
cBandsData = mirgetdata(cBands);
% Analysesignal
in Filterbereiche aufteilen
fBands = mirfilterbank(formant);
% Anzahl
der Frequenzbänder zwischenspeichern
numBands = length(cBandsData(1, 1, :));
% Bestimmen
der Hüllkurven der Bänder des Analysesignals
fBandsEnv = mirenvelope(fBands, 'Sampling',
44000, 'HalfwaveCenter', 'Lambda',
-0.001)
% Daten der Hüllkurven der Analysefilterbereiche
in eine Variable (fBandsEnvData) speichern
fBandsEnvData = mirgetdata(fBandsEnv);
% Gegebenenfalls
verlaengern des Traegersignals, falls es zu kurz ist
% und anpassen an die Laenge des Formantsignals
while length(cBandsData) < length(fBandsEnvData)
cBandsData = repmat(cBandsData, 2, 1);
end
cBandsData = cBandsData(1 : length(fBandsEnvData), :, :);
%
Frequenzbänder des Synthesesignals (cBandsData) mit Kanalhüllkurven
% des Formantsignals (fBandsEnvData) multiplizieren
bandsSum = cBandsData .* fBandsEnvData;
% Frequenzbänder wieder zusammenfuegen
sum = bandsSum(:, :, 1);
for i = 2:numBands
sum = sum + bandsSum(:, :, i);
end
% Ergebnis zu einem miraudio-Objekt machen
sumaudio = miraudio(sum, 44000);
% Ergebnis normalisieren
sumaudio = miraudio(sumaudio, 'Normal');
% Ergebnisabspielen
mirplay(sumaudio)
% Ergebnis im Spektrum anzeigen
mirspectrum(sumaudio, 'Frame', 'Min',
0, 'Max', 2000, 'NormalInput')
% Ergebnis abspeichern
mirsave(sumaudio, 'vocodiert')
% Ergebnis zur Ausgabe der Funktion machen
output = sumaudio;
und das Script über die Konsole in Matlab starten:
output_signal = vocoder('carrier.wav', 'formant.wav')
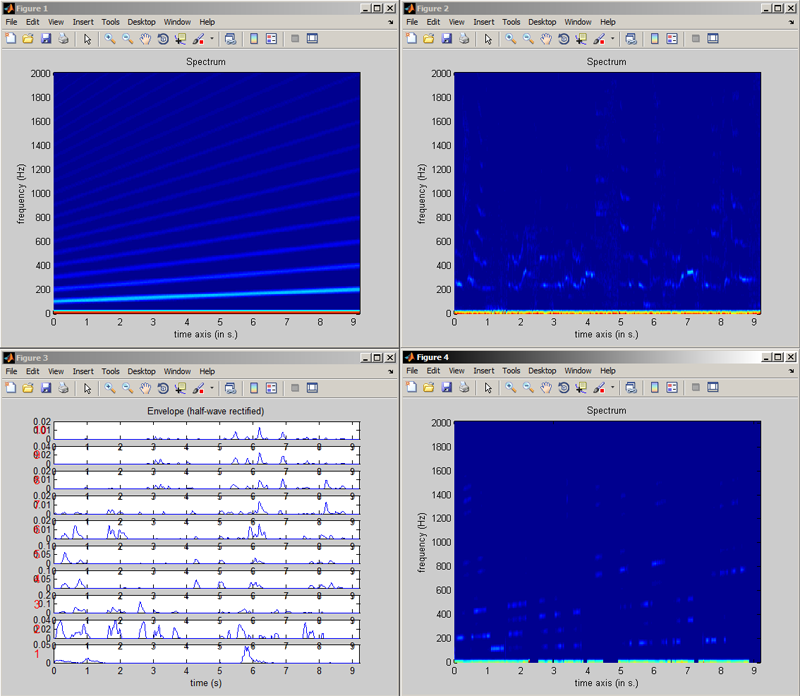
Wenn man als Synthesesignal (carrier) einen Sägezahn-Sweep nimmt und als Analysesignal (formant) ein Sprachbeispiel, dann zeigt sich insgesamt folgendes Ergebnis:
Überprüfung
der heute gängigen Timbre-Space-Modelle
ab
1975: John M. Grey: An Exploration of Musical Timbre, Diss. Stanford University
1975.
Versuchspersonen beurteilten die Ähnlichkeit von Instrumentalklangfarben (alle auf gleicher Tonhöhe, im Falle von Grey 1975: alle auf es' und resynthetisiert mit Line-Segment-Approximation)
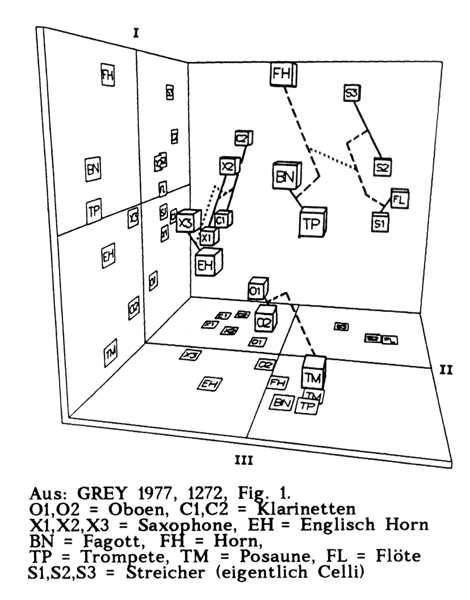
Eine mehrdimensionale Skalierung der Klangbeurteilungen im Vergleich mit den physikalischen Eigenschaften der Klänge resultierte in einem 3-dimensionalen timbre space mit 3 Achsen:
- Achse I: Schärfe
- Achse II: Fluktuationen im Spektrum
- Achse III: Einschwingvorgang (Vorläufergeräusche/töne)
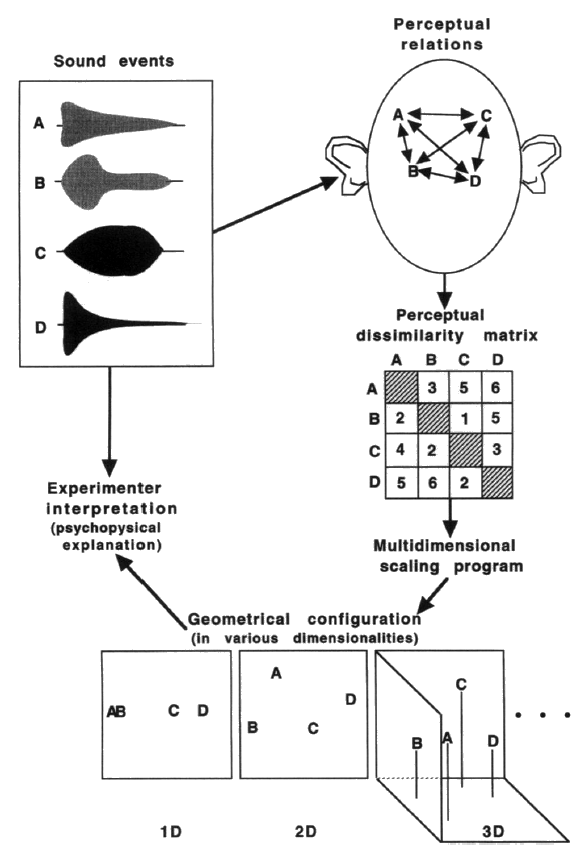
Schema, wie der Timbre space aufgrund von physikalischen
und psychoakustischen Merkmalen zustande kommt
(McAdams 1999, S. 87)
Je
nach Studie nehmen die gleichen „Instrumente” völlig
unterschiedliche
Positionen im Raum ein (GRY = Grey, KRH
= Krumhansl, McA = McAdams).
Selbst in den Timbre Spaces von Krumhansl und McAdams, die auf den
selben Stimuli basieren, nehmen die Klänge unterschiedliche
Positionen ein.
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
ab
2014: Siddiq, Saleh; Reuter, Christoph; Czedik-Eysenberg, Isabella: Kein
Raum für Klangfarben – Timbre Spaces im Vergleich.
In: Proceedings der 40. Jahrestagung für Akustik "Fortschritte
der Akustik", DAGA 2014, 10.-13. März, Oldenburg 2014, S. 56-57.
|
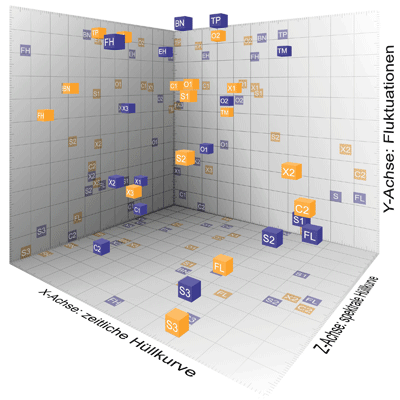
Alle
verwendeten Instrumente der verglichenen Timbre
Spaces wurden in einem gemeinsamen Meta Timbre
Space zusammengefasst: Dimensionen der verglichenen Timbre Spaces • X-Achse: Zeitliche Hüllkurve • Y-Achse: Spektrale Hüllkurve • Z-Achse: Spektrale Fluktuationen Grey, Krumhansl, McAdams |
|
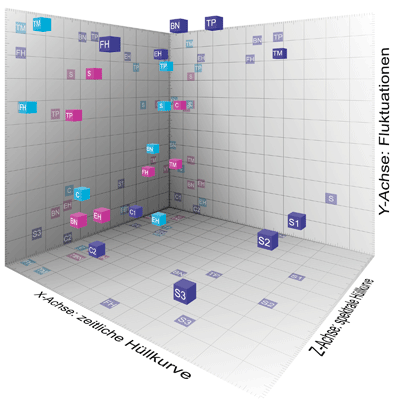
Vergleich
des perzeptiven Timbre Spaces von Grey mit einem errechneten Modell Errechnet
(Czedik-Eysenberg 2014) Dimensionen
der Timbre Spaces |
|
Replikationsstudie mit den Klängen Greys, Krumhansl/McAdams und der Vienna Symphonic Library (VSL). Nach
hierarchischer
Clusteranalyse zeigten sich drei Cluster: |
Ermittlung von Klangbeschreibungsmerkmalen (Timbre descriptors)
|
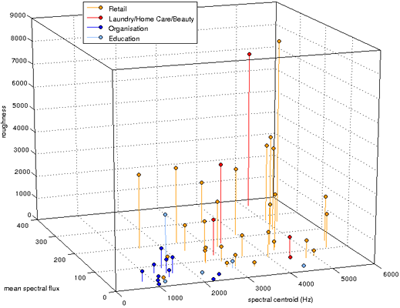
Matlab-Scripte zur Ermittlung von Klangbeschreibungsmerkmalen (Timbre descriptors): Mit Hilfe von Timbre-Deskriptoren lasssen sich verschiedene Klangfarbenmerkmale im gegenseitigen Zusammenhang darstellen (z.B. typische Klangmerkmale von Audiologos oder Spieldynamik in Abhängigkeit von Spektral Peak und Spectral Centroid) |
|
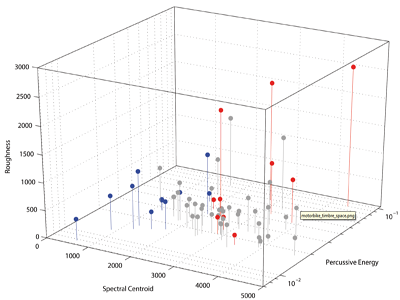
60
prototypische Motorradgeräusche wurden umfangreichen Signalanalysen
unterzogen, um eine Reihe von Klangeigenschaften zu extrahieren,
die mit der Lästigkeit der Klänge in Beziehung stehen
könnten. Ergebnis:
lästige Motorradklänge haben: |
|
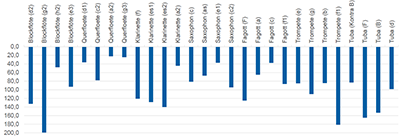
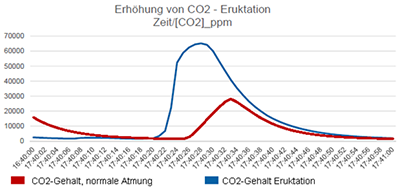
Was
passiert bei Eruktationen in Blasinstrumenten während des Spiels?
|
|
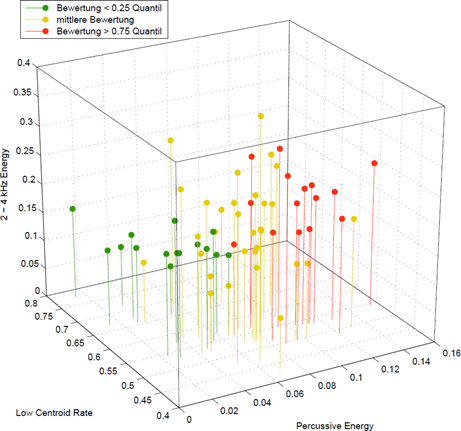
Was macht Musik „hart“? 62 Musikausschnitte wurden auf ihre Klangeigenschaften analysiert und von 40 Vpn auf ihre Härte hin bewertet. Gesangsstil und Anteil an perkussiver Energie lässt Rückschlüsse auf die Härte zu. Mit
Low Centroid Rate, Percussive Energy und 2-4 kHz Energy lässt
sich ein Meta-Deskriptor
"Härte" berechnen
|